Example Variables(Open Data):
The Fennema-Sherman Mathematics Attitude Scales (FSMAS) are among the most popular instruments used in studies of
attitudes toward mathematics. FSMAS contains 36 items. Also, scales of FSMAS have Confidence, Effectance Motivation,
and Anxiety. The sample includes 425 teachers who answered all 36 items. In addition, other characteristics of teachers,
such as their age, are included in the data.
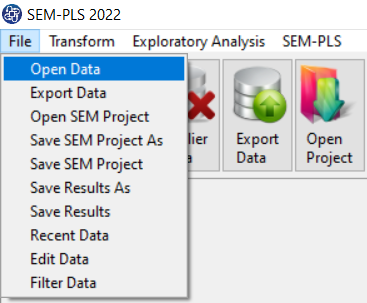
You can select your data as follows:
1-File
2-Open data
(See Open Data)
The data is stored under the name FSMAS-T(You can download this data from
here ).
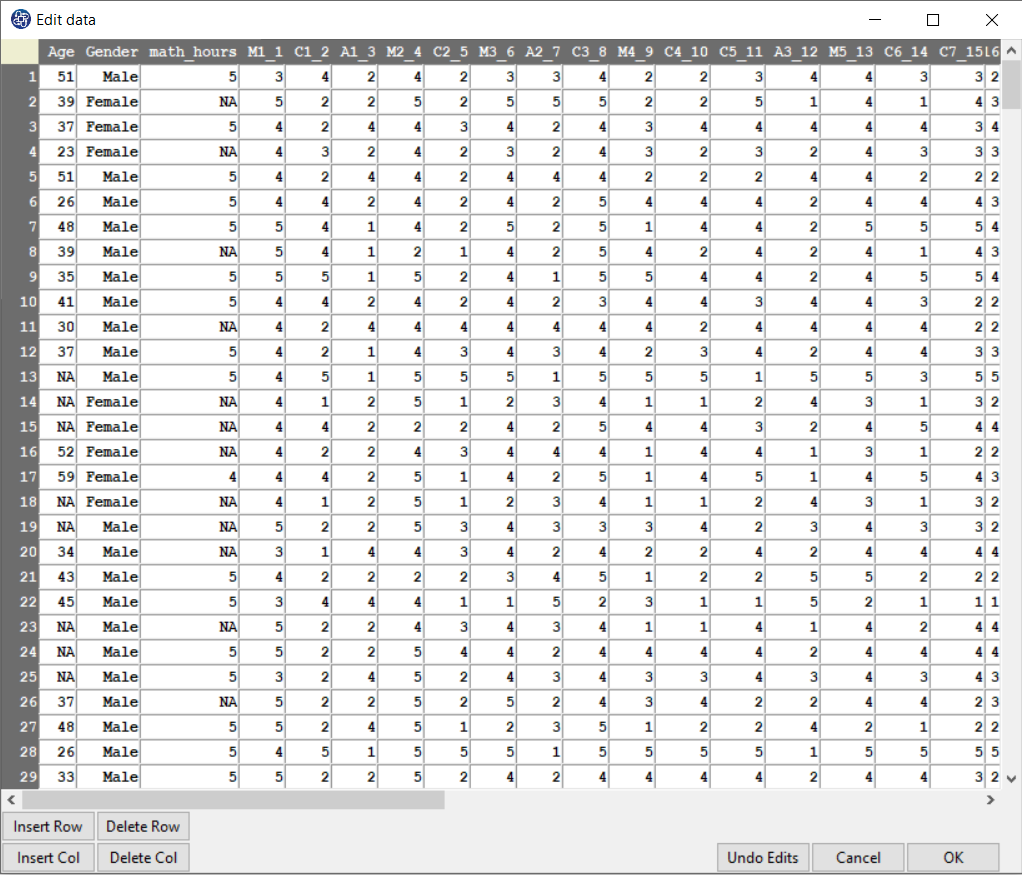
You can edit the imported data via the following path:
1-File
2-Edit Data
(See Edit Data)
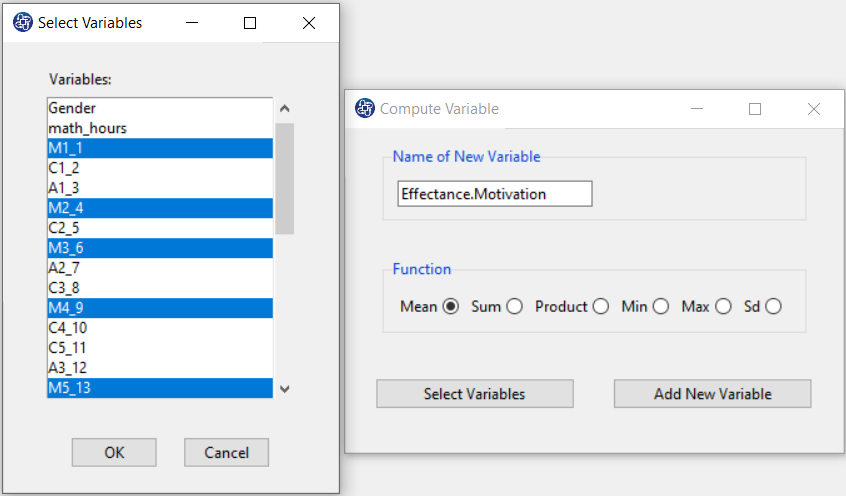
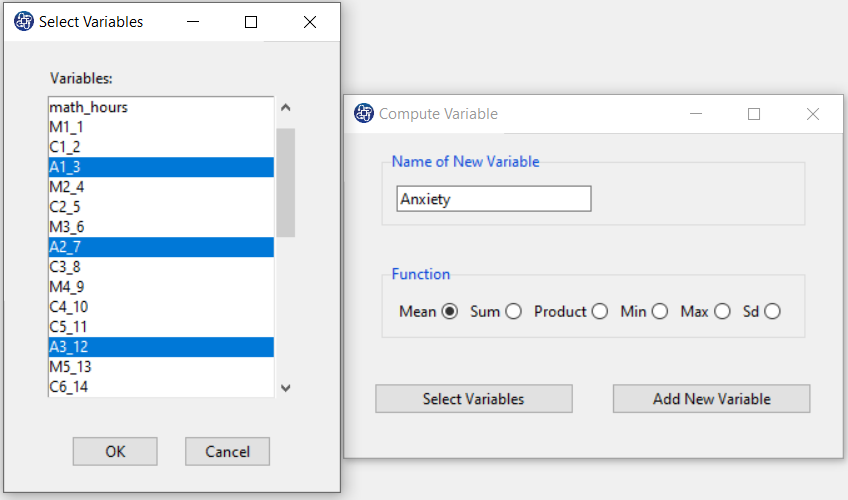
Example Variables(Compute Variable):
The three variables of Confidence, Effectance Motivation, and Anxiety can be calculated through the following path:
1-Transform
2-Compute Variable
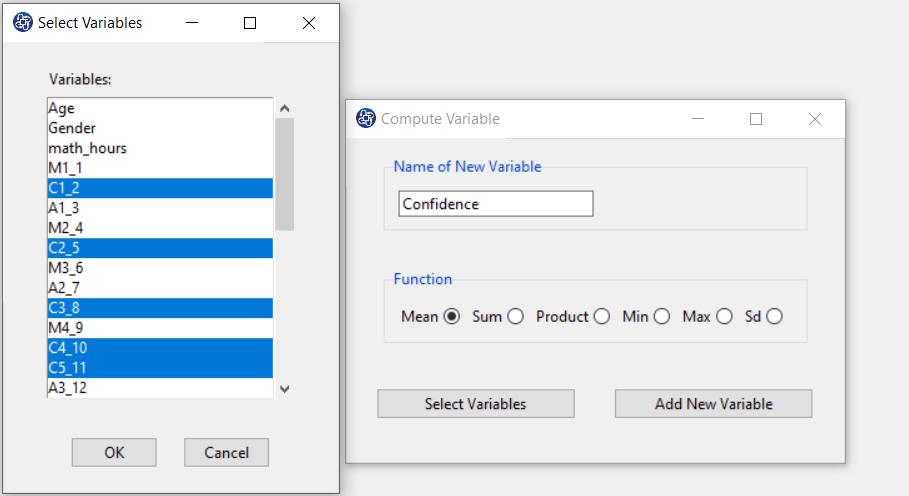
Items starting with the letters C, M, and A are related to the variables Confidence, Effectance Motivation, and Anxiety, respectively.
(See Compute Variable)
Introduction to MANOVA Regression:
The multivariate general linear model is
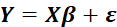where
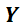is a matrix
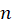cases on
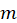dependent variables;
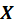is a model matrix with columns for
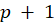regressors, typically including an initial column of 1s for the regression constant;
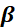is a matrix of regression coefficients, one column for each dependent variable; and
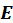is a matrix of errors.
The assumptions of the multivariate linear model concern the behavior of the errors:
Let
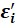represent the ith row of
.
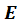Then
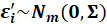where
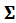is a nonsingular error-covariance matrix, constant across cases
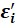and
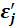are independent for
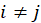and
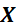is fixed or independent of
.
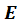We can write more compactly that
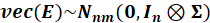. Here,
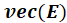ravels the error matrix row-wise into a vector, and
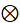is the Kronecker-product operator.
Paralleling the decomposition of the total sum of squares into regression and residual sums of squares in the univariate
linear model, there is in the multivariate linear model a decomposition of the total sum of squares and cross products
(SSP) matrix into regression and residual SSP matrices. We have
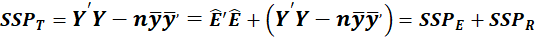
Path of MANOVA Regression:
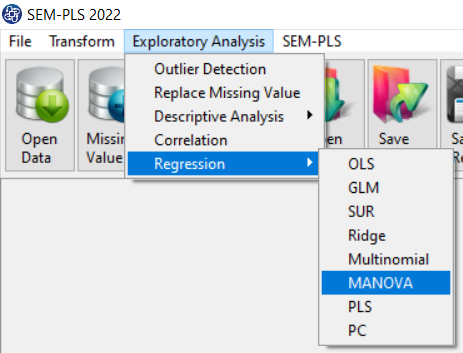
You can perform MANOVA regression by the following path:
1-Exploratory Analysis
2- Regression
3-MANOVA
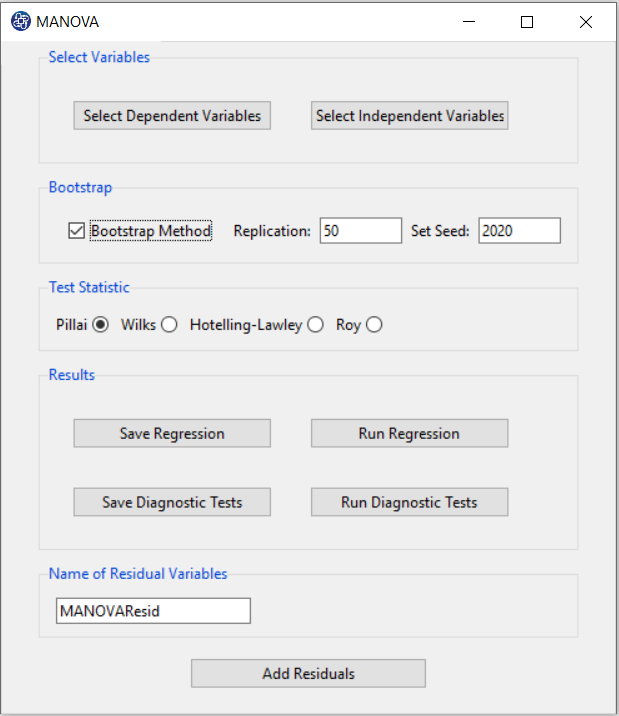
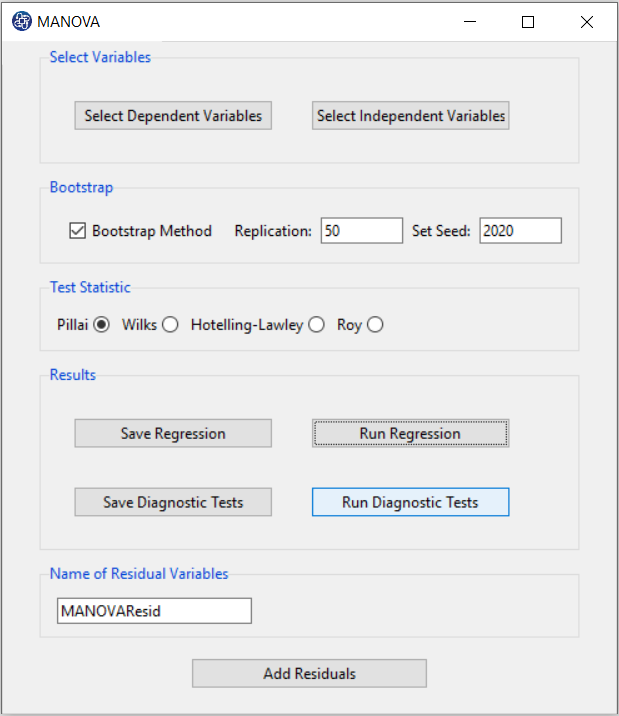
A. MANOVA window:
After opening the MANOVA window, you can start the model analysis process.
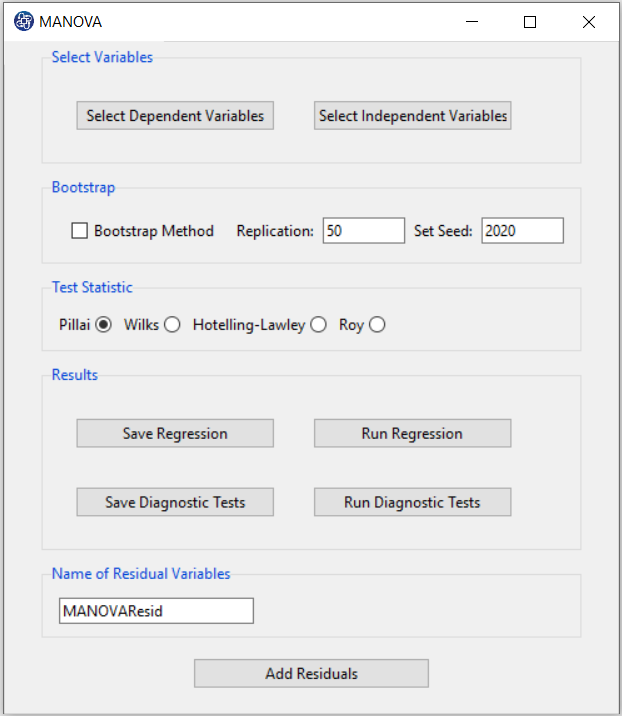
B. Select Dependent Variables:
You can select the dependent variables through this button. After opening the window, you can select it by selecting the desired variable.
For example, the variables Confidence and Effectance Motivation are selected in this data.
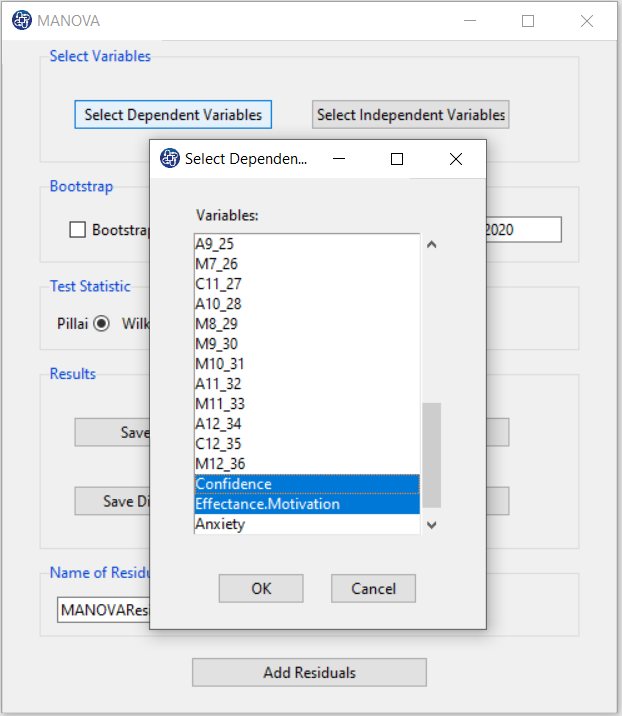
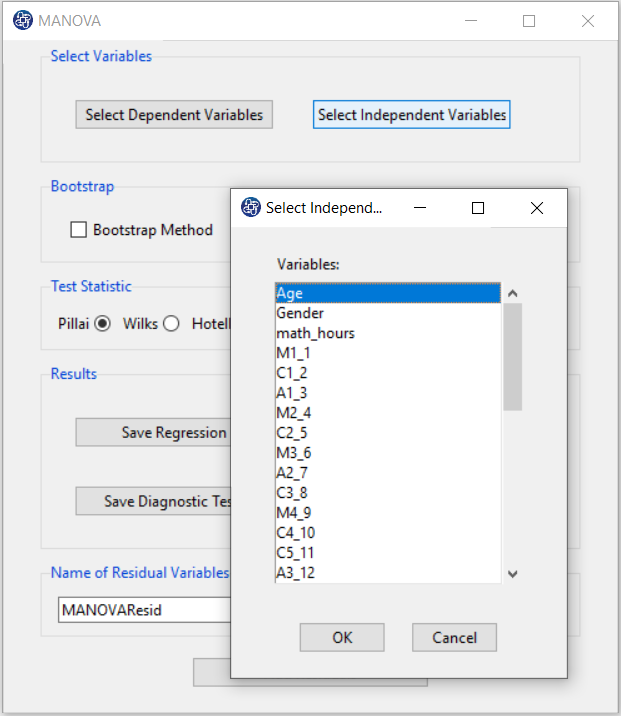
C. Select Independent Variables:
You can select the independent variables through this button.
After the window opens, you can select them by choosing the desired variables.
For example, Age and Anxiety is selected in this data.
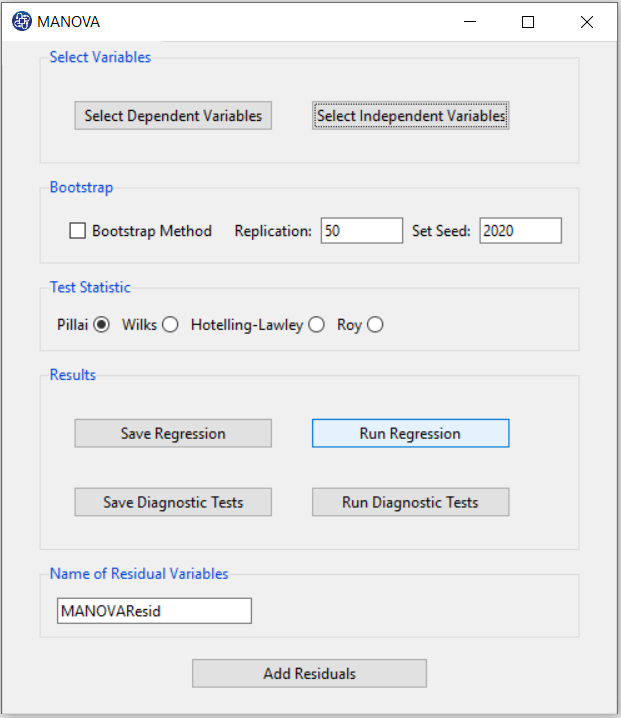
D. Run Regression:
You can see the results of the MANOVA regression in the results panel by clicking this button.
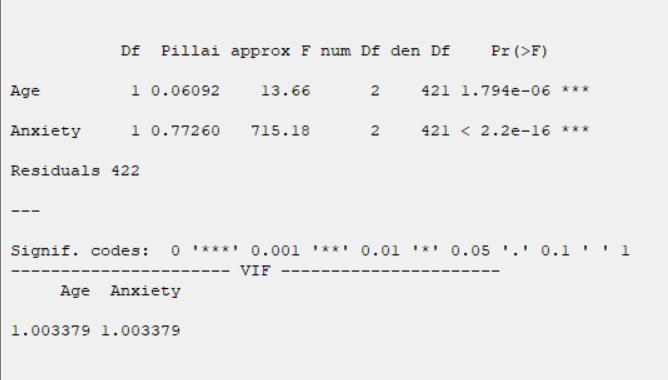
You can view the results based on that index by selecting one of the indexes presented in the Test Satistic panel.
D1. Test Satistic:
Let
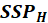represent the incremental
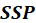matrix for a hypothesis. For
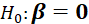, the
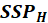matrix is
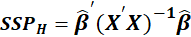
Multivariate tests for the hypothesis are based on the
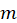eigenvalues
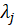of
.
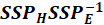The several commonly employed multivariate test statistics are functions of these eigenvalues:
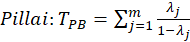
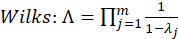
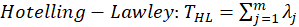
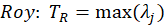
E. Results:
In the Parameter Estimates table, the results of estimating the coefficients of the independent variables are given.
The coefficients presented in this table are obtained from the following relationships:
* Test Statistic (
):
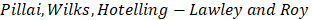The selected index value is presented in the Test Statistic option.
*approx. F , num Df, den Df , Pr(>F):
There are
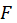approximations to the null distributions of these test statistics. For example, for Wilks’s Lambda, let
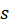represent the degrees of freedom for the term that we are testing (i.e., the number of columns of the model matrix
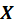pertaining to the term). Define
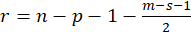
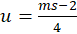
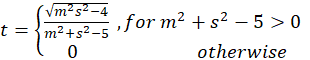
Under the null hypothesis
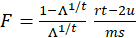follows an approximate
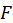distribution with
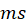and
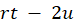degrees of freedom, and that this result is exact if
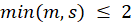(a circumstance under which all four test statistics are equivalent).
Thus, Pr(>F) is obtained from the following relation:
P-value=Pr(F>Fms, rt-2u)
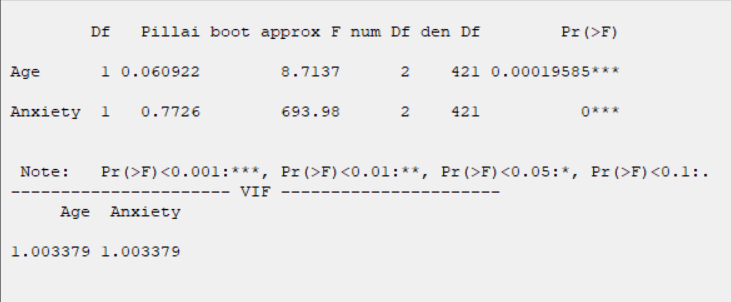
*Collinearity Diagnostics:
In the Collinearity Diagnostics table, the results of multicollinearity in a set of multiple regression variables are given.
For each independent variable, VIF index is calculated in two steps:
STEP1:
First, we run an ordinary least square regression that has xi as a function of all the other explanatory variables in the first equation.
STEP2:
Then, calculate the VIF factor with the following equation:
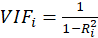
Where
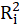is the coefficient of determination of the regression equation in step one. Also,
.
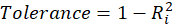A rule of decision making is that if
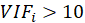then multicollinearity is high (a cutoff of 5 is also commonly used)
F. Save Regression:
By clicking this button, you can save the regression results. After opening the save results window, you can save the results in “text” or “Microsoft Word” format.
G. Bootstrap:
This option includes the following methods:
Assume that we want to fit a regression model with dependent variable y and predictors
x1, x2,..., xp. We have a sample of n observations zi = (yi,xi1, xi2,...,xip) where i= 1,...,n.
In random x resampling, we simply select B( Replication) bootstrap samples of the zi, fitting the model and saving the
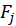and from each bootstrap sample. If
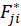is the corresponding estimate for the ith bootstrap replication, then the bootstrap
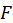is
.
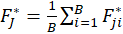*Bootstrap Method:
Enabling this option means performing regression using the bootstrap method with the following parameters:
*Replication: Number of Replication(B in equations)
*Set Seed: It is an arbitrary number that will keep the Bootstrap results fixed by holding it fixed.
G1. Results(Bootstrap):
Running regression with the Bootstrap option enabled provides the following results:
boot approx F
Pr(>F) based on approx F
H. Run Diagnostic Tests:
In MANOVA Regression, For each model, we shall make the following assumptions:
1-The residuals are independent of each other.
2- The residuals have a common variance
.
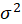3- It is sometimes additionally assumed that the errors have normal distribution.
For example, if the residuals are normal, the correlation test can replace the independence test.
The following tests are provided to test these assumptions:
* Test for Serial Correlation:
-Box Ljung:
The test statistic is:
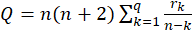
Where
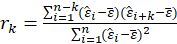
The sample autocorrelation at lag
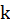and
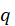is the number of lags being tested.
Under
,
.
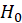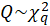In this software, we give the results for q=1.
*Test for Heteroscedasticity:
-Breusch Pagan:
The test statistic is calculated in two steps:
STEP1:
Estimate the regression:
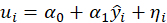
Where
,
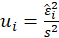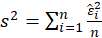
STEP2:
Calculate the
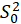test statistic:
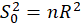
Under
,
.
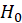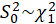*Normality Tests:
-Shapiro Wilk:
The Shapiro-Wilk Test uses the test statistic
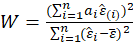
where the
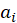values are given by:
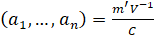
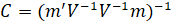
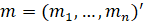is made of the expected values of the order statistics of independent and identically distributed random
variables sampled from the standard normal distribution; finally,
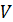is the covariance matrix of those normal order statistics.
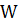is compared against tabulated values of this statistic's distribution.
-Jarque Bera:
The test statistic is defined as
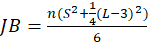
Where
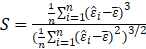
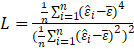
Under
,
.
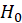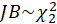-Anderson Darling:
The test statistic is given by:
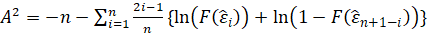Where F(⋅) is the cumulative distribution of the normal distribution.
The test statistic can then be compared against the critical values of the theoretical distribution.
-Cramer Von Mises:
The test statistic is given by:
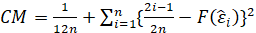where F(⋅) is the cumulative distribution of the normal distribution.
The test statistic can then be compared against the critical values of the theoretical distribution.
H1. Results(Diagnostic Tests):
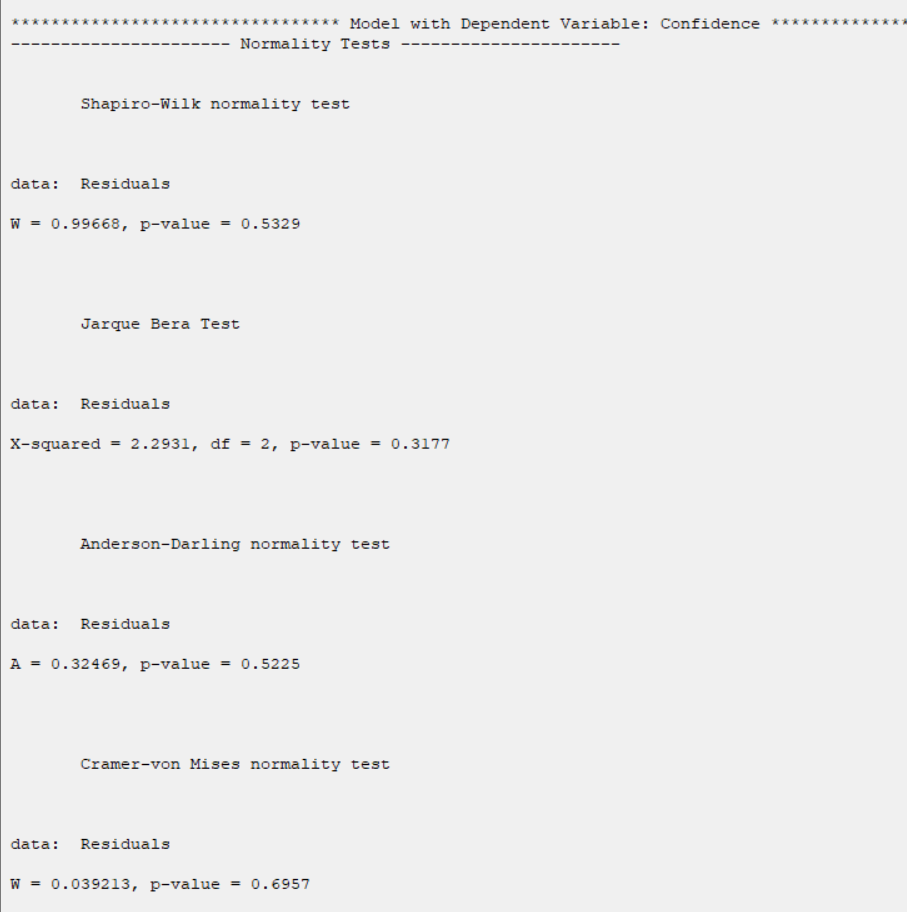
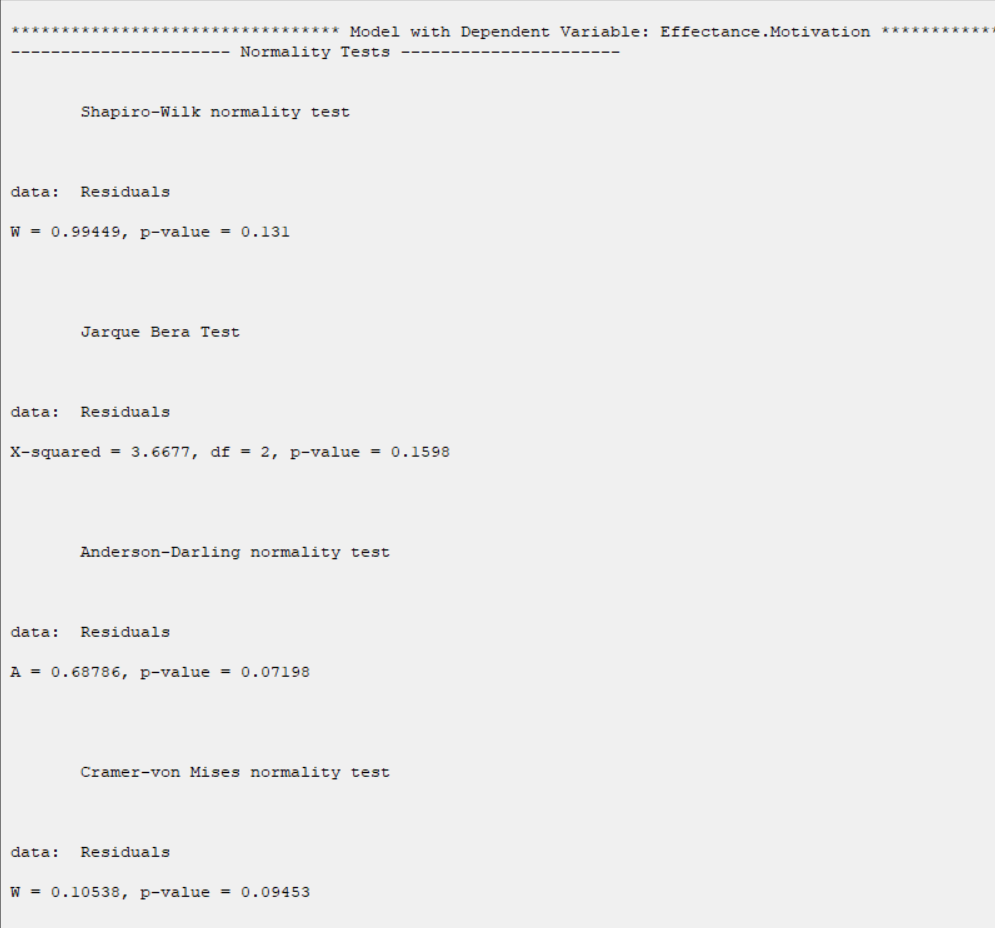
*Normality Tests:
The results show that in all tests the P-value is greater than 0.05. Therefore, at 0.95 confidence level, the normality of the residues of regression models is confirmed.
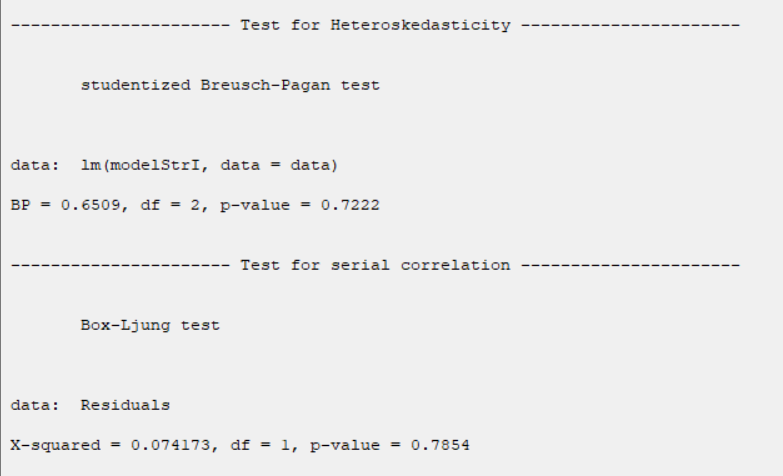
*Test for Heteroscedasticity:
The results show that in models with the dependent variable confidence,
the P-value is greater than 0.05. Also, in a model with dependent variable
Effectance Motivation, the P-value is smaller than 0.05.
Therefore, Only for confidence model residuals, 0.95 confidence level, the homogeneity of variance of residues is confirmed.
*Test for Serial Correlation:
The results show that in models with the dependent variable confidence, the P-value is greater than 0.05.
Also, in a model with dependent variable Effectance Motivation, the P-value is smaller than 0.05.
Therefore, Only for confidence model residuals, 0.95 confidence level, the independence of residues is confirmed.
H2. Save Diagnostic Tests:
By clicking this button, you can save the diagnostic tests results. After opening the save results window, you can save the results in “text” or “Microsoft Word” format.
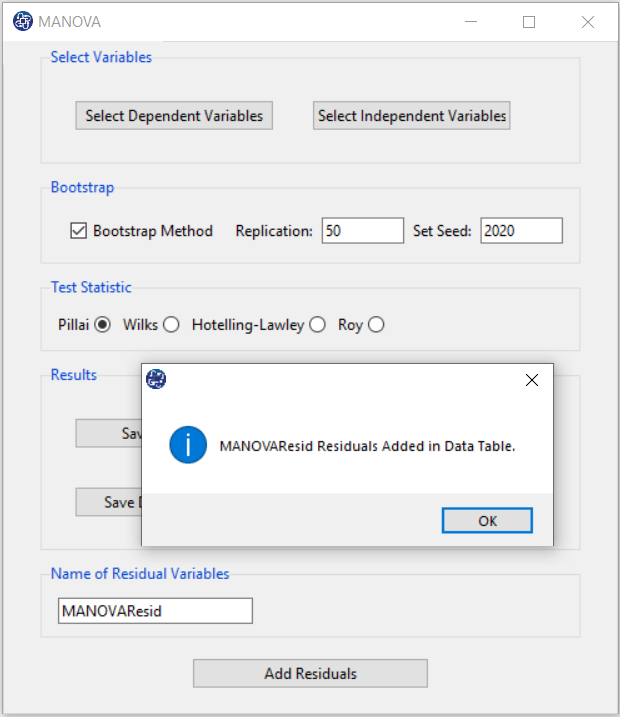
I. Add Residuals & Name of Residual Variable:
By clicking on Add Residuals button, you can save the residuals of the regression model with the desired name(Name of Residual Variable). The default software for the residual names is “MANOVAResid”.
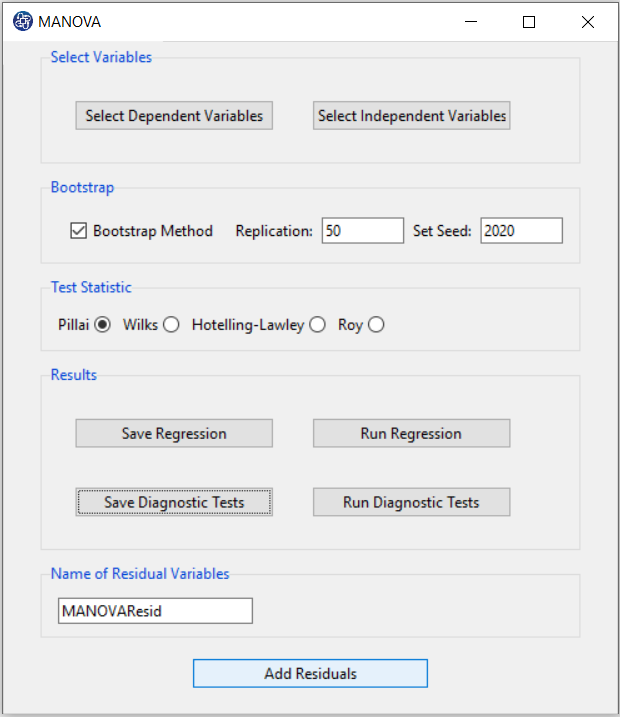
I1. Add Residuals(verify message):
This message will appear if the balances are saved successfully:
“Name of Residual Variable Residuals added in Data Table.”
For example,“MANOVAResid Residuals added in Data Table.”.
