Example Variables(Open Data):

The Fennema-Sherman Mathematics Attitude Scales (FSMAS) are among the most popular instruments used in studies of attitudes toward mathematics. FSMAS contains 36 items. Also, scales of FSMAS have Confidence, Effectance Motivation, and Anxiety. The sample includes 425 teachers who answered all 36 items. In addition, other characteristics of teachers, such as their age, are included in the data.
You can select your data as follows:
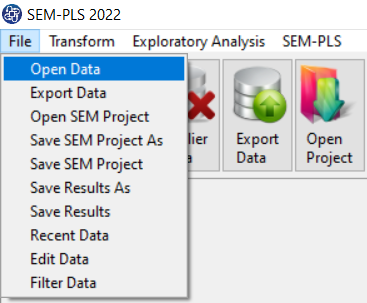
1-File
2-Open data
(See Open Data)

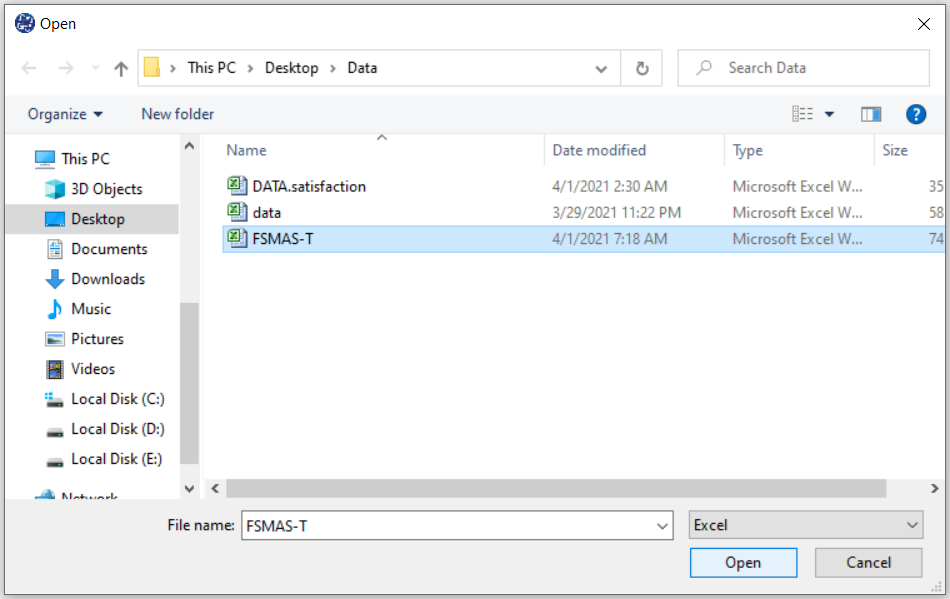
The data is stored under the name FSMAS-T(You can download this data from here ).
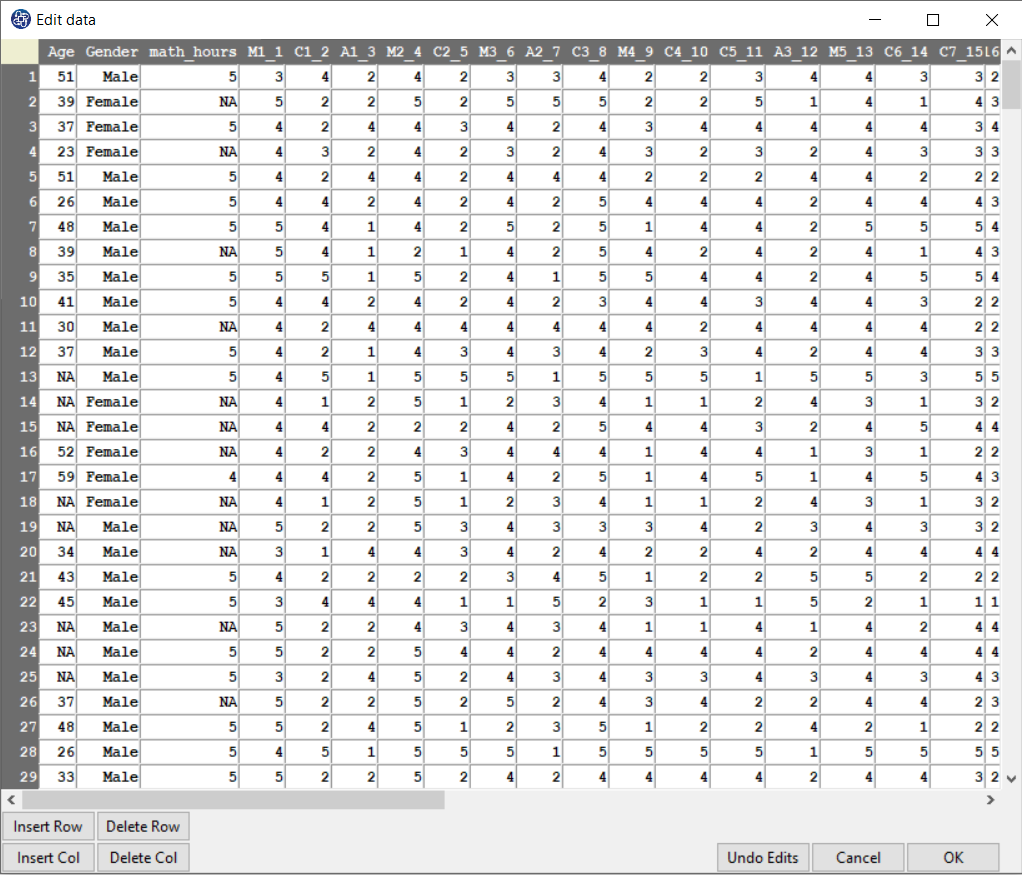
You can edit the imported data via the following path:
1-File
2-Edit Data
(See Edit Data)

Example Variables(Compute Variable):

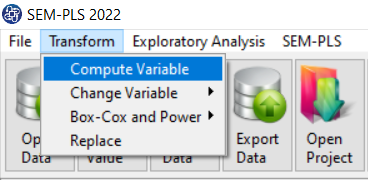
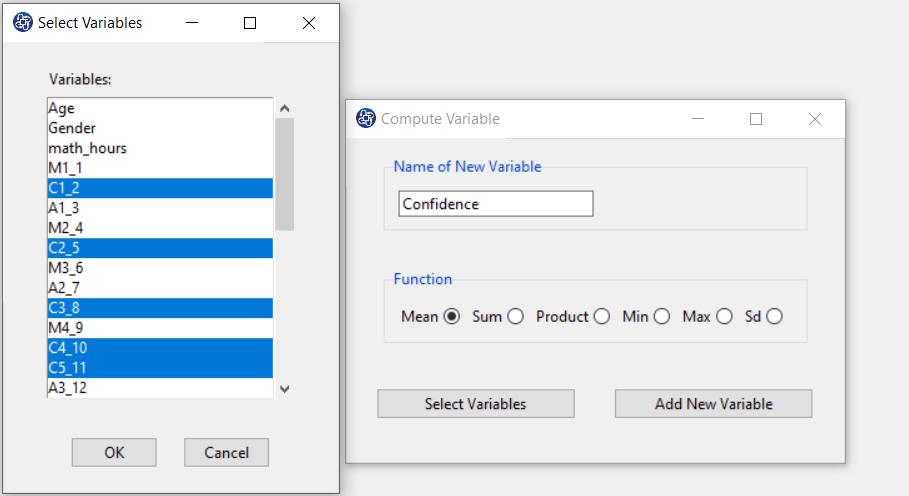
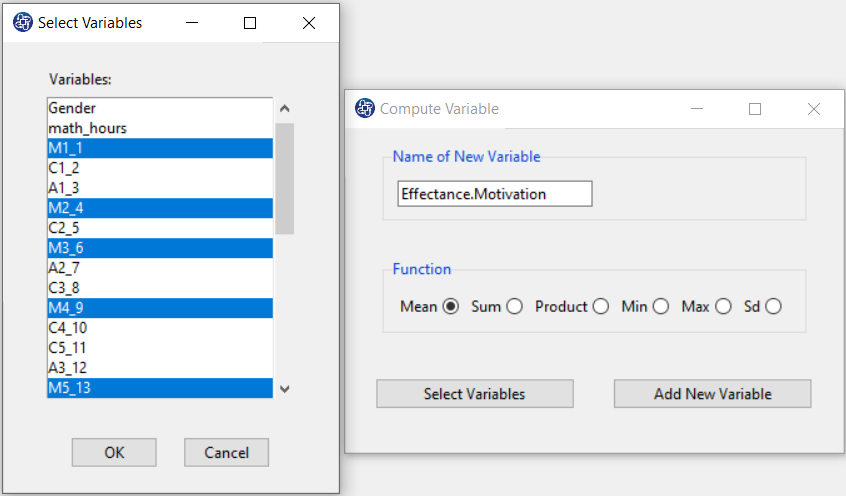
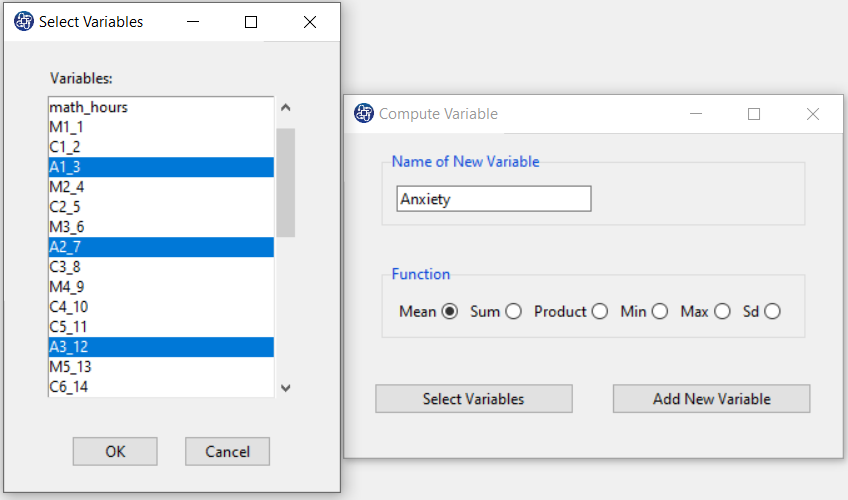
The three variables of Confidence, Effectance Motivation, and Anxiety can be calculated through the following path:
1-Transform
2-Compute Variable
Items starting with the letters C, M, and A are related to the variables Confidence, Effectance Motivation, and Anxiety, respectively.
(See Compute Variable)

Introduction to GLM Regression:

A generalized linear model (or GLM) consists of three components:
1-A random component, specifying the conditional distribution of the dependent variable, Y_i (for the i^th of n independently sampled observations), given the values of the independent variables in the model. In the initial formulation of GLMs, the distribution of Y_i was a member of an exponential family, such as the Gaussian, binomial, Poisson, gamma, or inverse-Gaussian families of distributions.

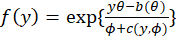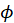Most commonly used statistical distributions are members of the exponential family of distributions whose densities can be written in the form Where is the dispersion parameter and 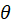is the canonical parameter.

It can be shown that




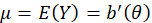
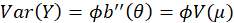
2- A linear predictor that is a linear function of regressors,

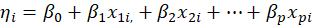
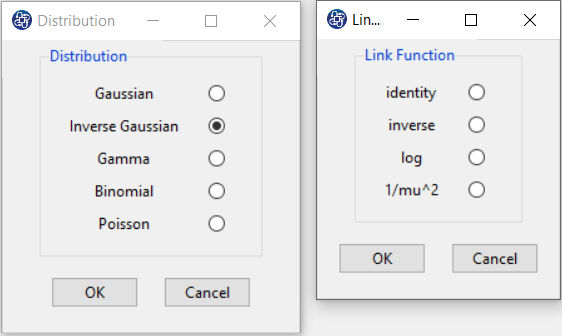
3-A smooth and invertible linearizing link function 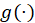, which transforms the expectation of the response variable, 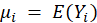, to the linear predictor: 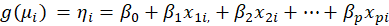, Because the link function is invertible, we can also write: 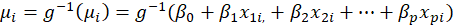Thus, the GLM may be thought of as a linear model for a transformation of the expected response or as a nonlinear regression model for the response.

Commonly employed link functions are shown in Table 1.

Table1:Some Common Link Functions

Link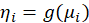
Identity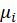
Log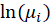
Inverse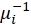
Inverse-square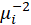
Square-root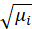
Logit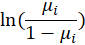
Probit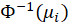
Complementary log-log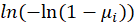
Cauchit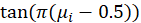

In Table1, 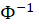is the cumulative distribution function of the standard normal distribution.
Also, Commonly employed distribution functions are:

*Gaussian (or Normal):
The Gaussian distribution with mean 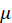and variance 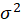has density function:


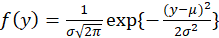
*Inverse Gaussian:
The inverse-Gaussian distributions are another continuous family indexed by two parameters, 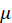and 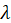, with density function

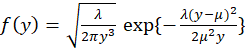
 Where 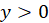 , 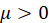is mean and .

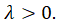*Gamma:
The gamma distributions are a continuous family with density function:

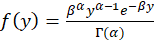
 Where 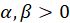 , , 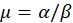and 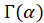is the gamma function. For all positive integers,

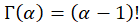
Binomial:
The binomial distribution for the proportion 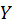of successes in n independent binary trials with probability of success 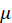has probability function

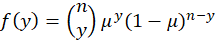
 Where  .

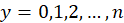*Poisson:
The Poisson distributions are a discrete family with probability function

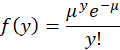
 Where  .

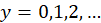*Estimation Algorithm:

A single algorithm can be used to estimate the parameters of an exponential family glm using maximum likelihood.
The log-likelihood for the sample 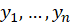is
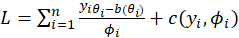
For 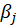, the maximum likelihood estimates are obtained by solving the score equations

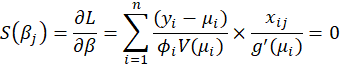
We assume that ,
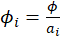where 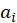are known prior weights.
A general method of solving score equations is the iterative algorithm Fisher’s Method of Scoring. In the r-th iteration, the new estimate 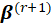is obtained from the previous estimate 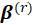. After calculations, 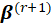is obtained from the following relation:

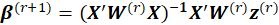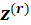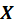i.e. the score equations for a weighted least squares regression of on with
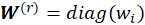
, where ,

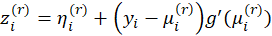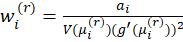
Hence the estimates can be found using an Iteratively Weighted Least Squares algorithm:

1-Start with initial estimates
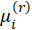
2-Calculate working responses 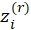and working weights
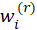
3-Calculate 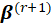by weighted least squares
4-Repeat 2 and 3 till convergence

For models with the canonical link, this is simply the Newton-Raphson method.
The estimates 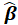have the usual properties of maximum likelihood estimators. In particular, 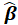is asymptotically .

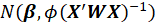Path of GLM Regression :

You can perform GLM regression by the following path:
1-Exploratory Analysis
2- Regression
3-GLM

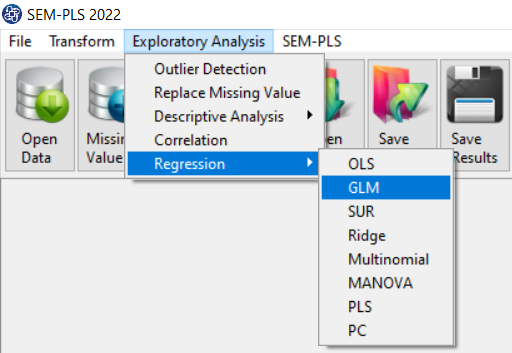
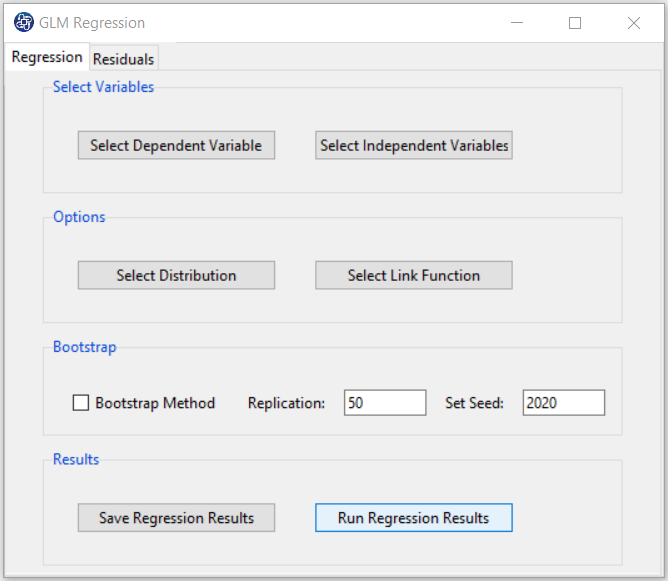
A. GLM Regression window:

GLM Regression panel includes two tabs, Regression and Residuals.

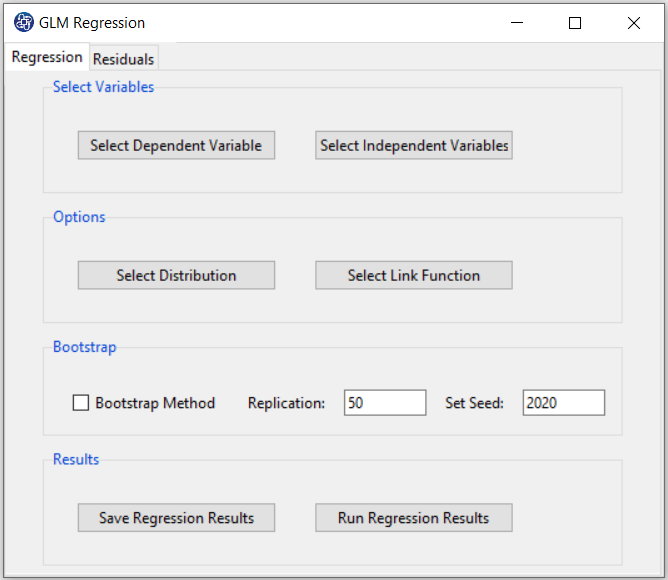
B. Regression

B1. Select Dependent Variable:

You can select the dependent variable through this button. After opening the window, you can select it by selecting the desired variable.
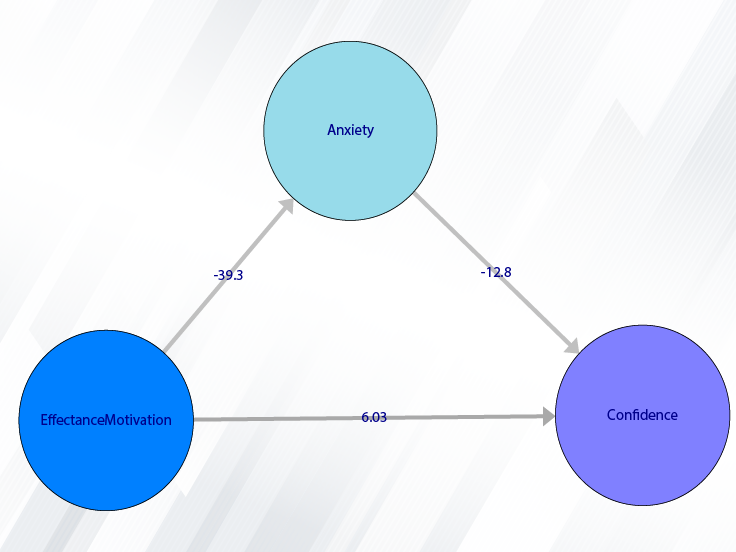
For example, the variable Confidence is selected in this data.

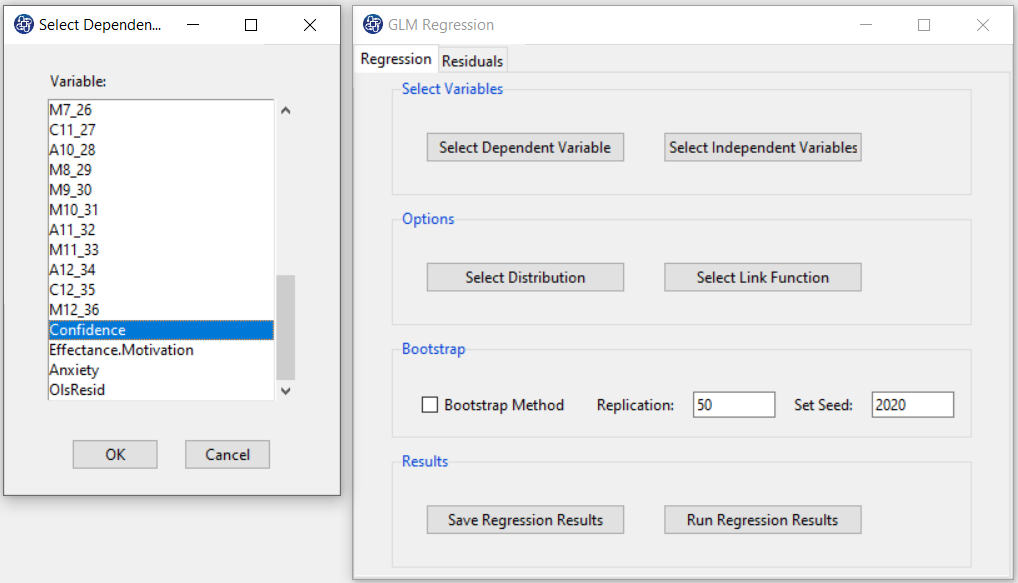
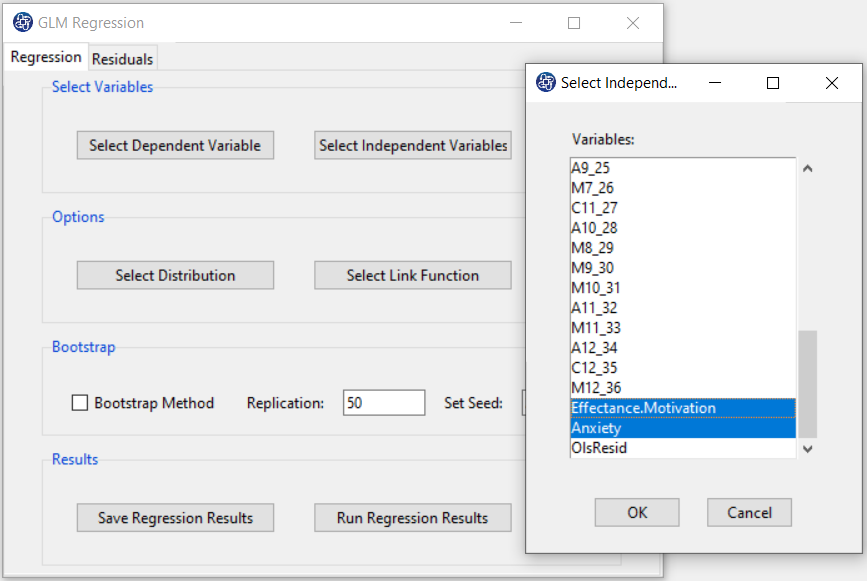
B2. Select Independent Variable:

You can select the independent variable through this button. After the window opens, you can select them by selecting the desired variables.
For example, the variables Effectance Motivation and Anxiety are selected in this data.

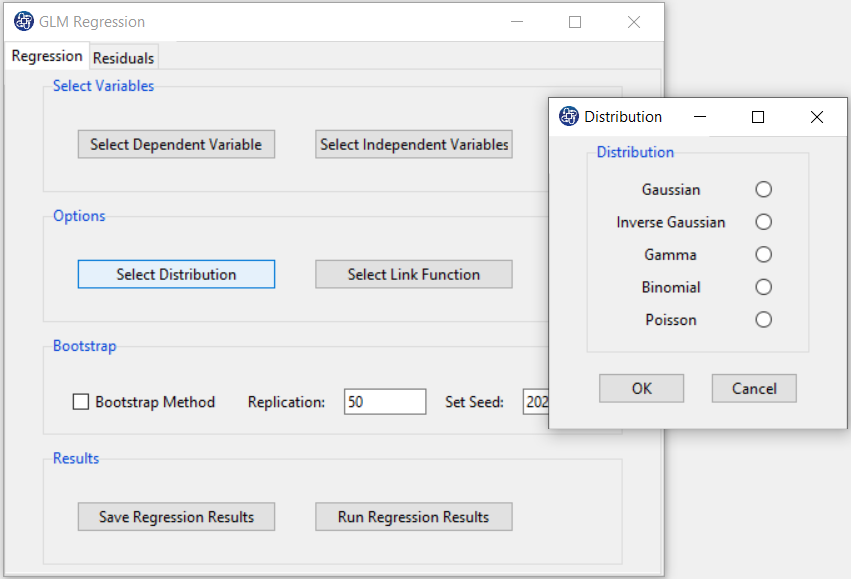
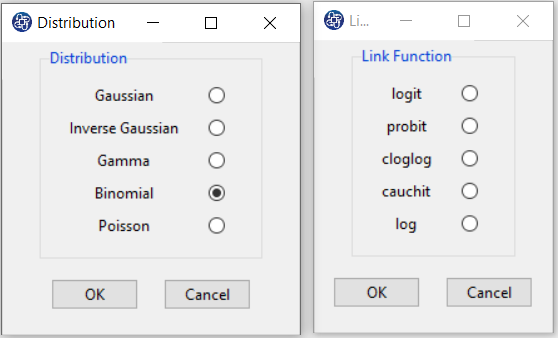
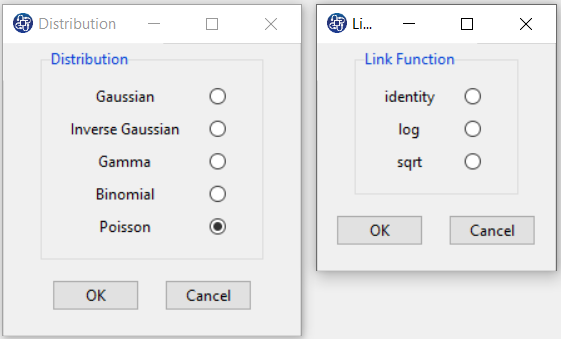
B3. Select Distribution:

After selecting the dependent and independent variables, you must select the appropriate distribution with the dependent variable type. You can select one of the following distributions:
-Gaussian (or Normal)
-Inverse Gaussian
-Gamma
-Binomial
-Poisson

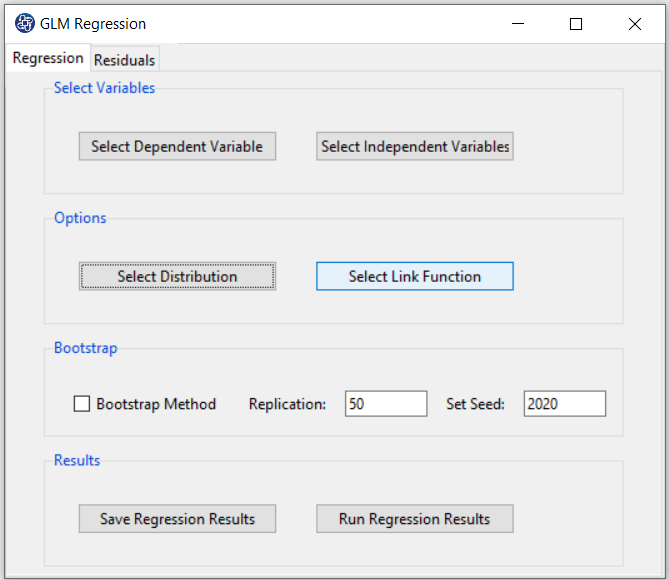
B4. Select Link Function:

After selecting the distribution, you must choose one of the suggested link functions.

B4.1. Gaussian distribution:

The following link functions are suggested for Gaussian distribution:

Link
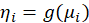
Identity
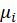
Inverse
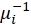
Log

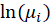
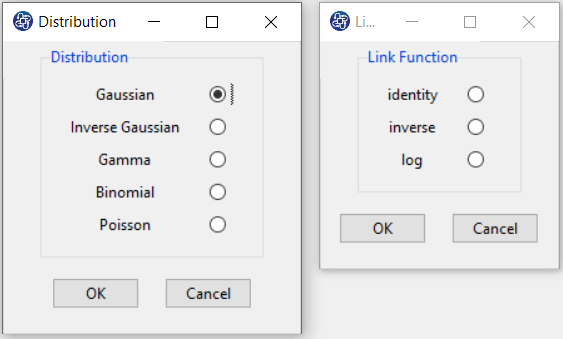
B4.2. Inverse Gaussian distribution:

The following link functions are suggested for Inverse Gaussian distribution:

Link
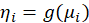
Identity
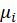
Inverse
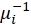
Log
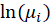
Inverse-square

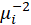
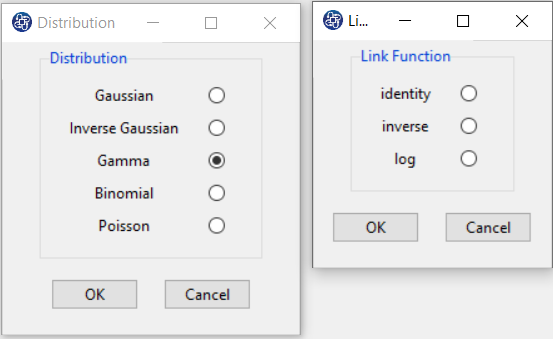
B4.3. Gamma distribution:

The following link functions are suggested for Gamma distribution:

Link
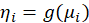
Identity
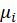
Inverse
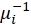
Log

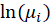
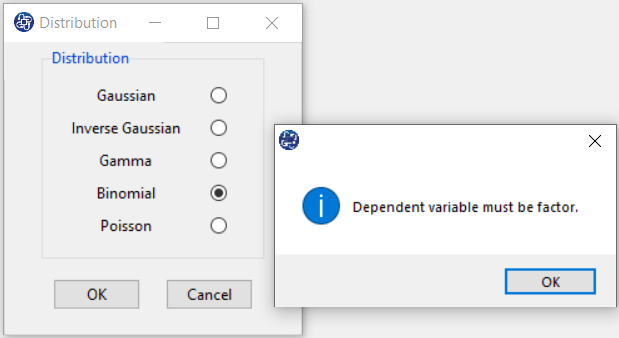
B4.4. Error:

The type of distribution must be proportional to the type of dependent variable.
For example, to select a binomial distribution, the dependent variable needs to be a factor. If you select another variable (Like gender) of type factor, you can choose one of the Binomial or Poisson options.

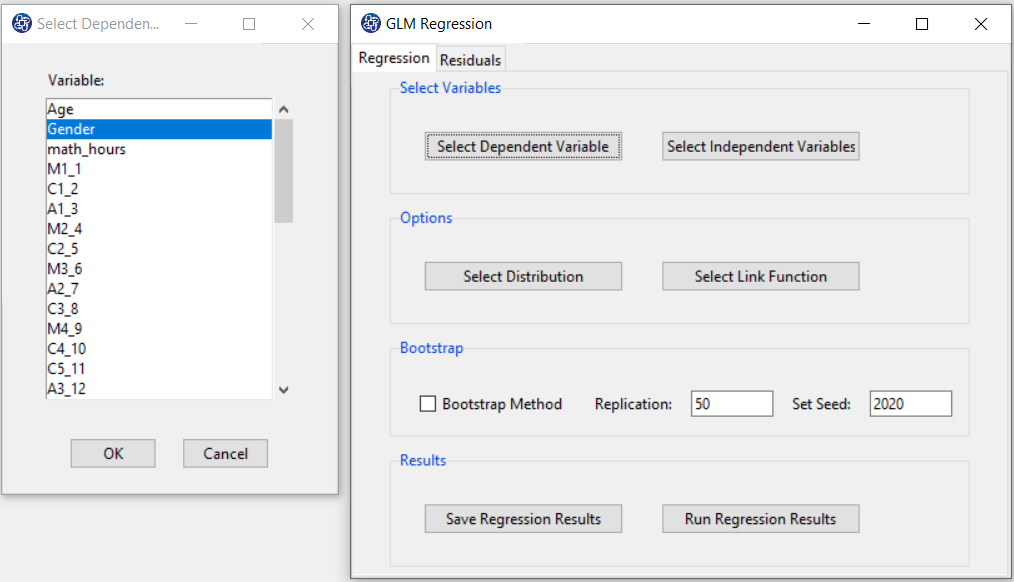
B4.5. Binomial distribution:

The following link functions are suggested for Binomial distribution:

Link
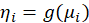
Logit
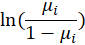
Probit
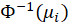
Complementary log-log
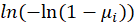
Cauchit
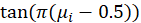
Log

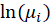
B4.6. Poisson distribution:

The following link functions are suggested for Poisson distribution:

Link
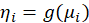
Identity
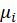
Log
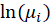
Inverse

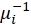
B5. Run Regression:

You can see the results of the GLM regression in the results panel by clicking this button.
Results include the following:
-Deviance Residuals
-Coefficients
-AIC
-VIF

B5.1. Results:

Results include the following:

*Deviance Residuals:
A five-number summary of the deviance residuals is given. This part of the results includes Min(minimum of residuals), 1Q(first quartile of residuals), Median(median of residuals), 3Q(third quartile of residuals), and Max(maximum of residuals).

Coefficients:
The coefficients presented in this table are obtained from the following relationships:

*Beta:


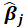
*Std. Error:


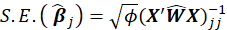
*z value:
For non-Normal data, we can use the fact that asymptotically


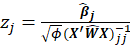
*Pr(>|z|):
P-Value=Pr(| 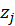|>z)

* Different model summaries are reported for GLMs. First, we have the deviance of two models: Null deviance, Residual deviance.
The first refers to the null model in which all of the terms are excluded, except the intercept if present. The degrees of freedom for this model are the number of data n minus 1 if an intercept is fitted. The second two refer to the fitted model, which has a n-p degree of freedom, where p is the number of parameters, including any intercept.
The deviance of a model is defined as
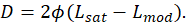
where 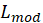is the log-likelihood of the fitted model and 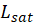is the log-likelihood of the saturated model.

*AIC:
The AIC is a measure of fit that penalizes for the number of parameters p


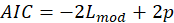
*VIF:
In the Collinearity Diagnostics table, the results of multicollinearity in a set of multiple regression variables are given.
For each independent variable, the VIF index is calculated in two steps:
STEP1:
First, we run an ordinary least square regression that has xi as a function of all the other explanatory variables in the first equation.
STEP2:
Then, calculate the VIF factor with the following equation:
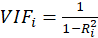
Where 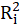is the coefficient of determination of the regression equation in step one. Also,
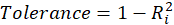
A rule of decision making is that if 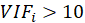then multicollinearity is high (a cutoff of 5 is also commonly used)

B6. Save Regression:

By clicking this button, you can save the regression results. After opening the save results window, you can save the results in “text” or “Microsoft Word” format.

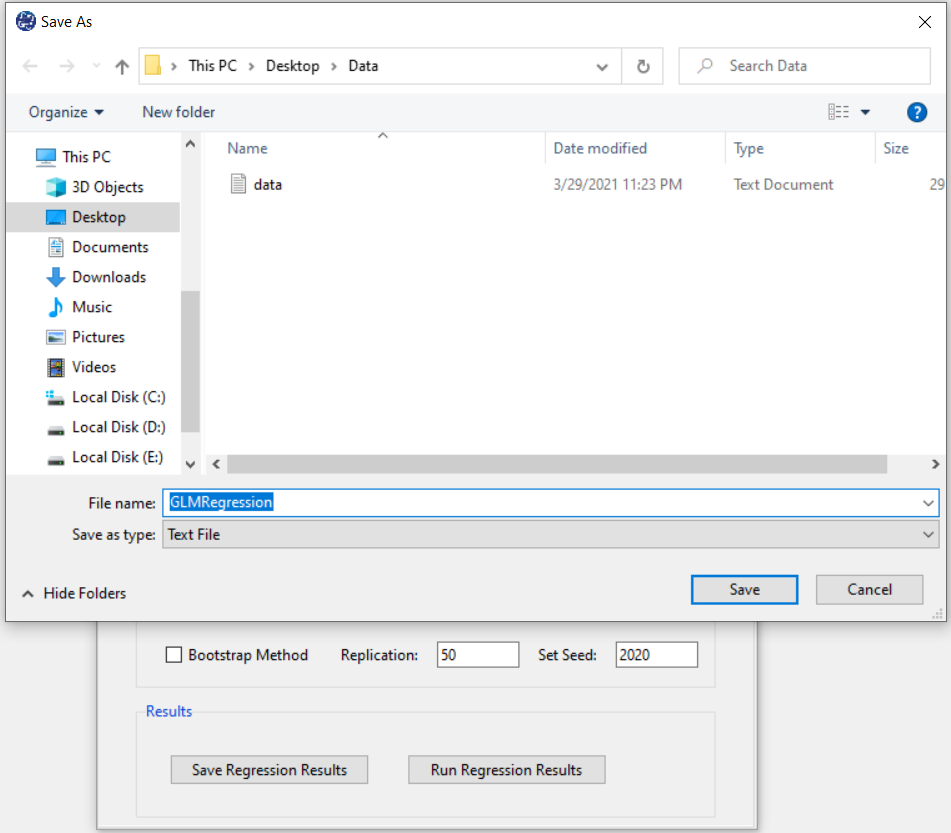
B7. Bootstrap:

This option is located in the Regression tab. This option includes the following methods:
Assume that we want to fit a regression model with dependent variables y and predictors x₁, x₂,..., x_p. We have a sample of n observations z_i = (y_i,x_i1, x_i2,...,x_ip) where i= 1,...,n. In random x resampling, we simply select B(Replication) bootstrap samples of the z_i, fitting the model and saving the 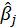and 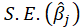and from each bootstrap sample. The statistic t is normally distributed (which is often approximately the case for statistics in sufficiently large Replication ). If 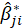is the corresponding estimate for the 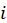bootstrap replication and 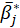is the mean of the 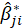s , then the bootstrap estimation and the bootstrap standard error are

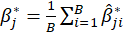
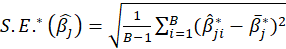
Thus

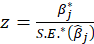
*Bootstrap Method:
Enabling this option means performing regression using the bootstrap method with the following parameters:

*Replication: Number of Replication(B in equations)
*Set Seed: It is an arbitrary number that will keep the Bootstrap results fixed by holding it fixed.

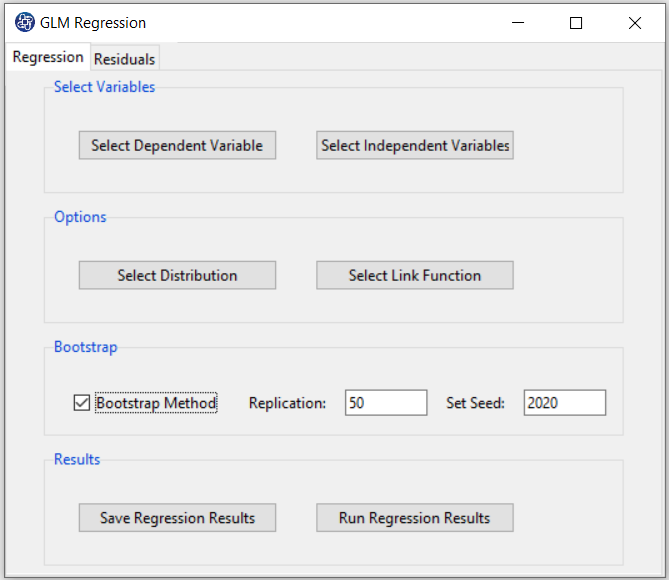
B7.1. Results(Bootstrap):

Running regression with the Bootstrap option enabled provides the following results: Original:
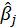
bootCoefficient:
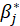
bootSE:
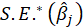
z value: z value

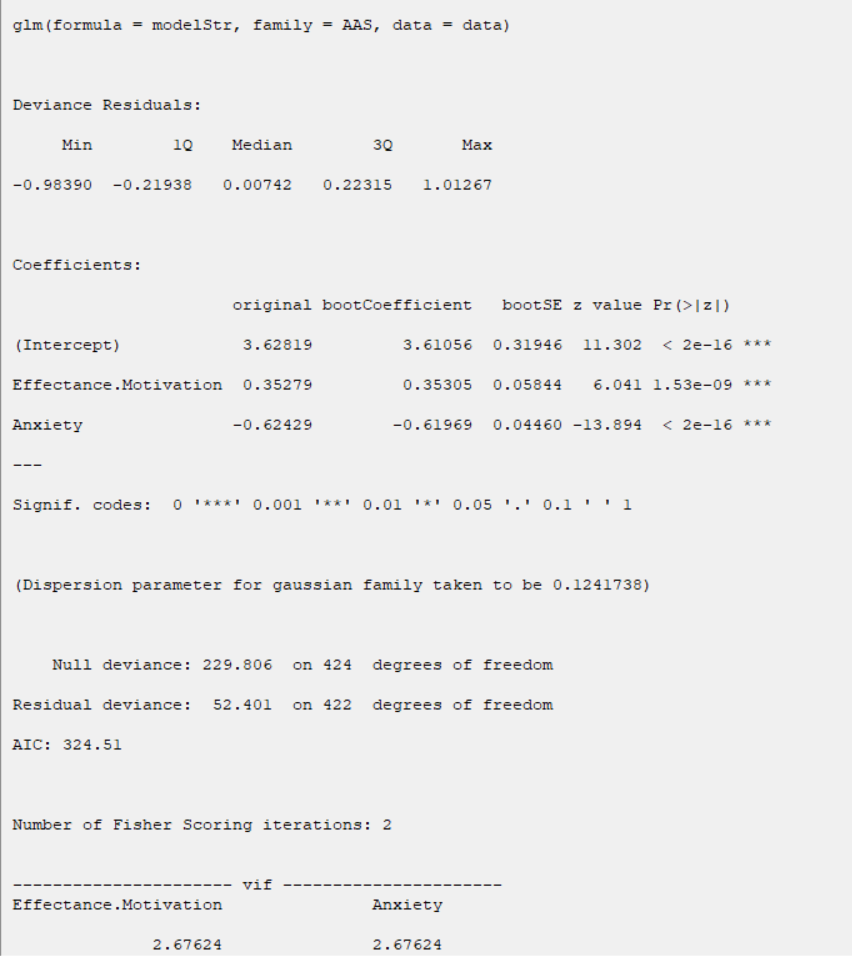
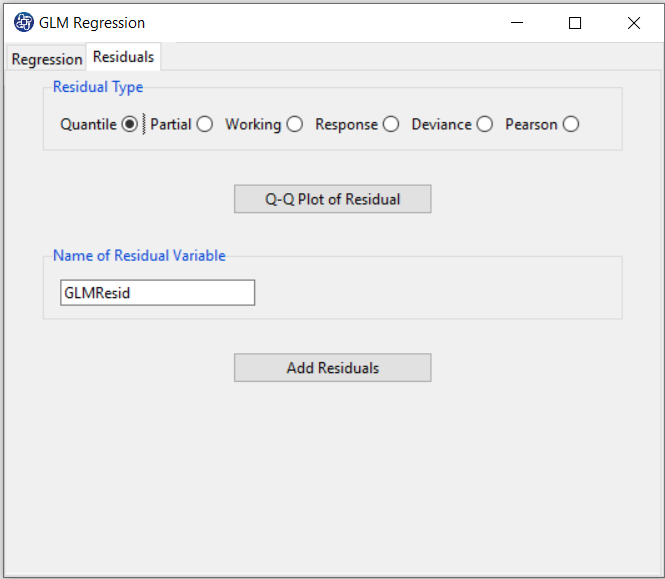
C. Residual

C1. Residual Type:

In the Residual tab, the Residual Type panel includes a variety of residues. Several kinds of residuals can be defined for GLMs:

*Quantile: The quantile residual for observation has the same cumulative probability on a standard normal distribution as y does for the fitted distribution.

*Partial: Partial residuals plots are similar to plotting residuals against 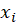, but with the linear trend with respect to 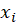added back into the plot.

*working: from the working response in the IWLS algorithm.

*response:

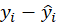
*Deviance:

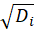
*Pearson:

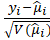
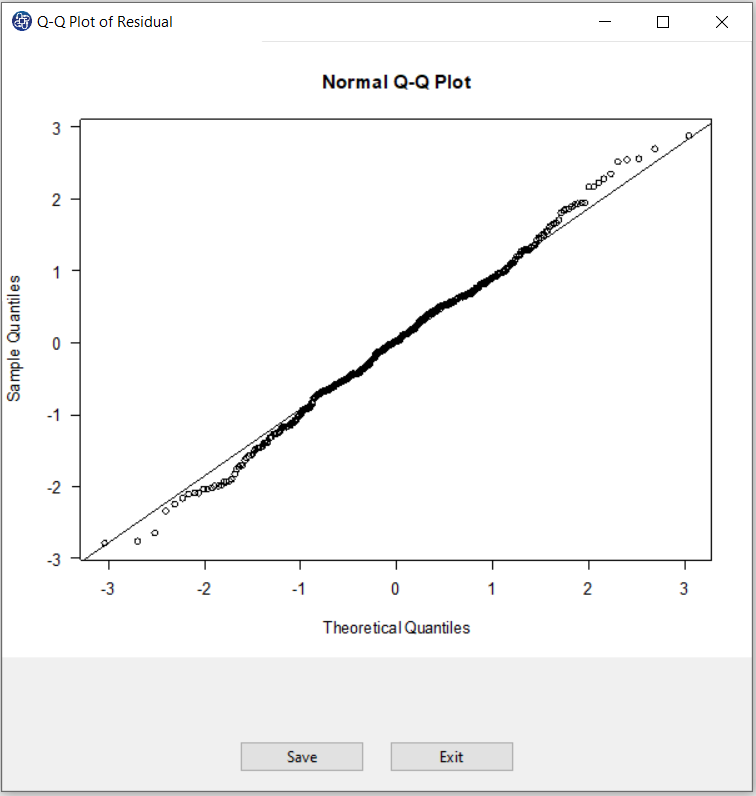
C2. QQ Plot of Residuals:

After selecting the Residual Type, by clicking on the QQ Plot of Residuals button, you can assess the normality of the residues. If the residuals follow a normal distribution with mean 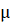and variance 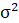, then a plot of the theoretical percentiles of the normal distribution(Theoretical Quantiles) versus the observed sample percentiles of the residuals(Sample Quantiles) should be approximately linear. If a Normal QQ Plot is approximately linear, we assume that the error terms are normally distributed.

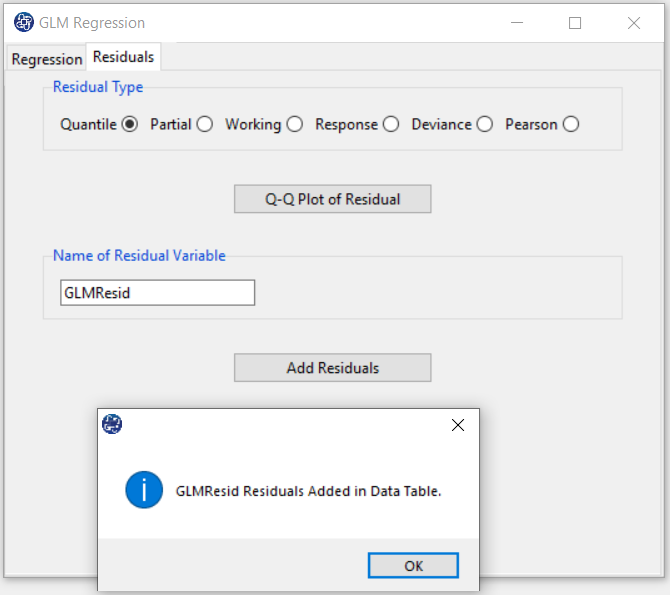
C3. Add Residuals & Name of Residual Variable:

By clicking on the “Add Residuals” button, you can save the Residuals of the regression model with the desired name (Name of Residual Variable). The default software for the residual names is “GLMResid”.
This message will appear if the balances are saved successfully:
“Name of Residual Variable Residuals added in Data Table.”
For example,“GLMResid Residuals added in Data Table.”.