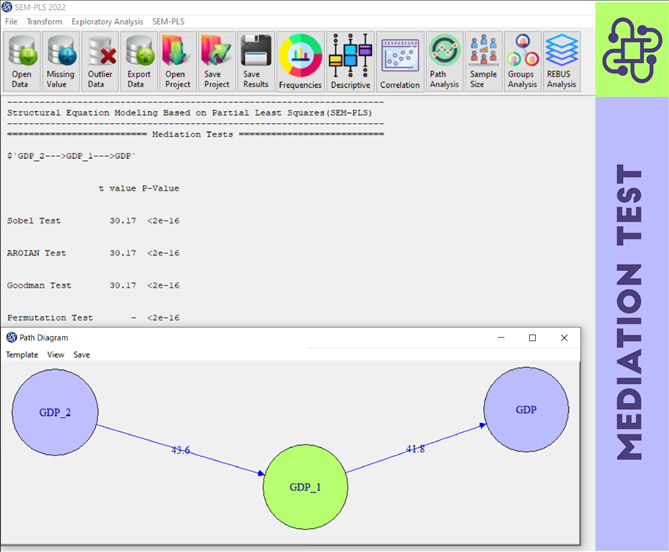
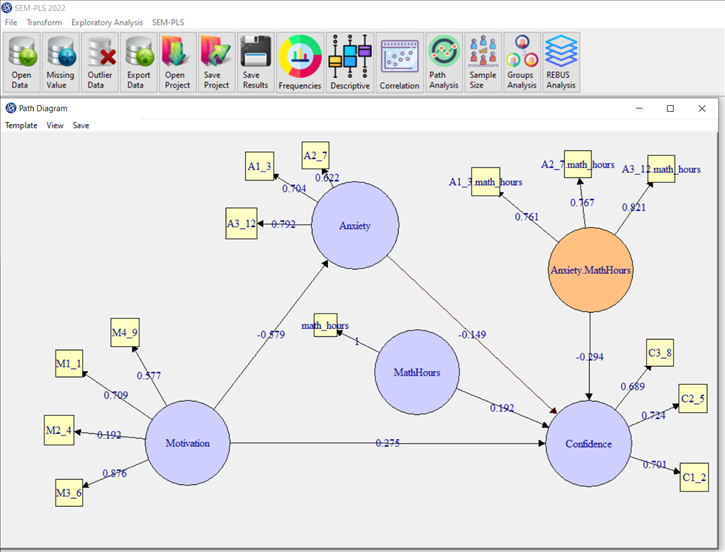
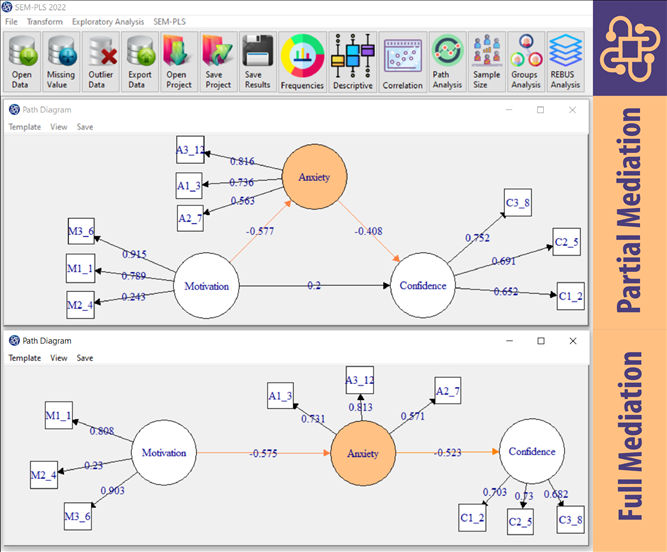
Many datasets are far from being a homogenous mass of data. Diversity is the rule. More often than not, you will find subsets of observations with a particular behavior; perhaps there is a subset that shows different patterns in the distribution of the variables, or maybe there are observations that could be grouped and analyzed separately. It might well be the case that one single model is not the best model for your entire dataset, and you might need to estimate different SEM-PLS models for other groups of observations.
When we estimate the SEM-PLS model, we do it under the implicit assumption that all the observations in the data are more or less homogeneous. This implies that we treat all observations alike without considering any group structure, and we take for granted that a single model will adequately represent all the individuals. Consequently, we suppose that the same set of parameter values applies to all observations. The problem, however, is that this assumption may not be realistic in all cases; and it is reasonable to expect diversity in our data. This diversity in data receives the special name of heterogeneity.
People say that heterogeneity can be observed or unobserved. When we have information characterizing groups in data like gender, ethnic group, or income level, we talk about observed heterogeneity. In contrast, we talk about unobserved heterogeneity when we don’t have such variables or any other information about the causes of diversity. This may sound a little complicated, but it is just a term to say that we don’t have the slightest idea of what the heck is causing diversity in our data.
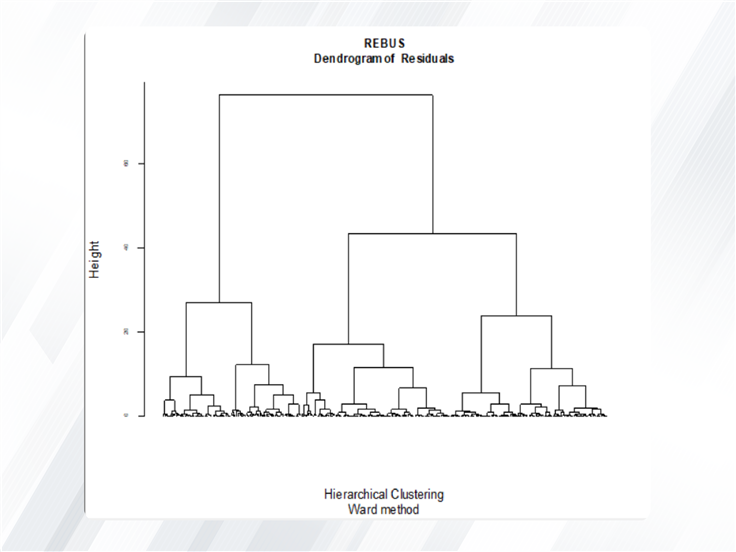
You can analyze this issue using the REBUS method(See Introduction to SEM-PL: E.4.3. REBUS (Response Based Unit Segmentation)). The REBUS is the acronym for Response Based Unit Segmentation in SEM-PLS, and it is an approach based on an algorithm designed to discover latent classes inside an SEM-PLS model.
The SEM-PLS software allows you to do REBUS in different ways. With this software, in addition to comparing the path coefficients in other groups, you can perform model indices such as R-Squared, GOF, etc.(See REBUS Analysis.).